Lyapunov functions for positive linear evolution

Cooperation with: L. Schimansky-Geier (Humboldt-Universität zu Berlin), E.Y. Khruslov (B. Verkin Institute for Low Temperature Physics and Engineering, Kharkov, Ukraine)

Supported by: DFG: ``Physikalische Modellierung und numerische Simulation von Strom- und Wärmetransport bei hoher Trägerinjektion und hohen Temperaturen'' (Physical modeling and numerical simulation of current and heat transport at high carrier injection and high temperatures)

Description: Lyapunov functions for evolution equations are important tools for their variational formulation and the asymptotic investigation of the underlying problem. As usual, for a given equation we have a special Lyapunov function. So, it is well known (see, e.g., [2]) that the classical Fokker-Planck equation

$\displaystyle {\frac{{\partial}}{{\partial t}}}$ W(z, t) = ( $\displaystyle \bf A^{*}_{}$ W)(z)

- $\displaystyle \sum\limits_{{i=1}}^{n}$ $\displaystyle {\frac{{\partial}}{{\partial z_i}}}$ $\displaystyle \Big($ a_i(z)W $\displaystyle \Big)$ + $\displaystyle \sum\limits_{{i,j=1}}^{n}$ $\displaystyle {\frac{{\partial^2}}{{\partial z_i\partial z_j}}}$ $\displaystyle \Big($ b_ij(z)W $\displaystyle \Big)$

(1)

H(t) = H[W₁, W₂] = $\displaystyle \int_{\Gamma}^{}$ W₁(z, t)log $\displaystyle {\frac{{W_1(z,t)}}{{W_2(z,t)}}}$ dz ,

(2)

Equation (1) describes the evolution of the probability density W(z, t) of a Markov process z(t) in phase space z(t) $\subset$ $\Gamma$ $\subset$ $\IR^{n}_{}$ . As usual, equation (1) is considered in L₁-type spaces, for instance L₁( $\Gamma$ , dz), where it has (under certain assumptions) a unique normalized positive solution W(z, t) $\geq$ 0, | W(^., t)|_L₁ = 1, if the initial density W₀(z) is positive and normalized.

In general, e.g., if the coefficients of (1) degenerate b_ij(z) $\geq$ 0, the densities can vanish somewhere or they may not exist at all. In this case it is difficult to understand what is H(t), defined by (2), and to show ${\frac{{d}}{{dt}}}$ H(t) $\leq$ 0 in a rigorous way. Furthermore, it is natural to ask if there are other Lyapunov functions of (1) and what other equations of this type have Lyapunov functions. These problems can be solved completely by an inequality for Radon measures ([3]) in the following way:

Let $\Gamma$ be a compact topological Hausdorff space, $\cal {C}$ ( $\Gamma$ ) the space of continuous real-valued functions on $\Gamma$ , and $\cal {C}$ ^*( $\Gamma$ ) (the dual of $\cal {C}$ ( $\Gamma$ )) the space of regular Radon measures, $\cal {C}$ ^**( $\Gamma$ ) the bidual of $\cal {C}$ ( $\Gamma$ ), and $\langle$ ^.,^. $\rangle$ their dual pairing.

Let $\cal {S}$ ^* = {p $\in$ $\cal {C}$ ^*( $\Gamma$ ) : p $\geq$ 0,| p| = 1} be the convex set of positive and normalized (i.e. probability) measures in $\cal {C}$ ^*( $\Gamma$ ) and $\cal {S}$ _e^* = $\big\{$ $\delta_{z}^{}$ $\big\vert$ z $\in$ $\Gamma$ $\big\}$ the subset of extreme points of $\cal {S}$ ^*.

Let $\bf S$ be a linear Markov operator in $\cal {C}$ ( $\Gamma$ ), i.e. an operator with $\bf S$ $\geq$ 0 and $\bf S$ 1 = 1, and $\bf S^{*}_{}$ its adjoint. $\cal {S}$ ^* is invariant with respect to adjoint Markov operators.

Theorem 1: Let p, q $\in$ $\cal {S}$ ^*, $\bf S^{*}_{}$ the adjoint of a Markov operator and F(x) : $\IR_{+}^{}$ $\longrightarrow$ $\IR$ a convex function with F(1) = 0. Let q/p be the Radon-Nikodym derivative of q by p and H[p, q] : = $\left<\vphantom{F \left( q/p \right), p }\right.$ F $\left(\vphantom{ q/p }\right.$ q/p $\left.\vphantom{ q/p }\right)$ , p $\left.\vphantom{F \left( q/p \right), p }\right>$ , then the following inequality holds: 0 $\leq$ H[ $\bf S^{*}_{}$ p, $\bf S^{*}_{}$ q] $\leq$ H[p, q]. Equality holds if $\bf S^{*}_{}$ maps extreme points to extreme points $\bf S^{*}_{}$ $\cal {S}$ _e^* $\subset$ $\cal {S}$ _e^*.

From this inequality one can derive Lyapunov functions for linear evolution equations for probability measures. Let $\bf A$ be the generator of a continuous semigroup in $\cal {C}$ ( $\Gamma$ ), satisfying $\bf A$ 1 = 0 and the maximum principle, i.e. ( $\bf A$ g)(z₊) $\leq$ 0 for g $\in$ D( $\bf A$ ), where z₊ is the max-point of g (i.e. g(z) $\leq$ g(z₊), z $\in$ $\Gamma$ ). Then, it is well known ([1]) that the evolution equation

$\displaystyle \dot{{p}}$ (t) = $\displaystyle \bf A^{*}_{}$ p(t), p(0) = p₀ $\displaystyle \in$ $\displaystyle \cal {S}$ ^*

(3)

Theorem 2: Let p₀, q₀ $\in$ $\cal {S}$ ^* and H[p₀, q₀] : = $\left<\vphantom{F \left( q_0/p_0 \right), p_0 }\right.$ F $\left(\vphantom{ q_0/p_0 }\right.$ q₀/p₀ $\left.\vphantom{ q_0/p_0 }\right)$ , p₀ $\left.\vphantom{F \left( q_0/p_0 \right), p_0 }\right>$ exist. Let p(t) and q(t) be two solutions to equation (3) with p(0) = p₀ and q(0) = q₀. Then H[p(t), q(t)] exists for all times and satisfies 0 $\leq$ H[p(t₂), q(t₂)] $\leq$ H[p(t₁), q(t₁)], t₂ $\geq$ t₁. If equation (3) is the Liouville equation of a dynamical system $\dot{{z}}$ = $\Phi$ (z) with solution in $\cal {C}$ ( $\Gamma$ ), then equality holds, i.e. the function H(t) = H[p(t), q(t)] is constant in time.

If q = q is any stationary solution, we get 0 $\leq$ H[p(t₂), q] $\leq$ H[p(t₁), q] for t₂ $\geq$ t₁.

If $\Gamma$ $\subset$ $\IR^{n}_{}$ , then the general form of operators $\bf A$ , satisfying the maximum principle, is

$\displaystyle \big($ $\displaystyle \bf A$ g $\displaystyle \big)$ (z)

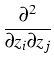$\displaystyle \sum\limits_{{i=1}}^{n}$ a_i(z) $\displaystyle {\frac{{\partial}}{{\partial z_i}}}$ g + $\displaystyle \sum\limits_{{i,j=1}}^{n}$ b_ij(z) $\displaystyle {\frac{{\partial^2}}{{\partial z_i\partial z_j}}}$ g + - $\displaystyle \int_{\Gamma}^{}$ Q(z, z') $\displaystyle \Big($ g(z') - g(z) $\displaystyle \Big)$ dz'

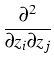$\displaystyle {\frac{{\partial}}{{\partial t}}}$ W(z, t)	=	- $\displaystyle \sum\limits_{{i=1}}^{n}$ $\displaystyle {\frac{{\partial}}{{\partial z_i}}}$ $\displaystyle \Big($ a_i(z)W $\displaystyle \Big)$ + $\displaystyle \sum\limits_{{i,j=1}}^{n}$ $\displaystyle {\frac{{\partial^2}}{{\partial z_i\partial z_j}}}$ $\displaystyle \Big($ b_ij(z)W $\displaystyle \Big)$ +
	+	- $\displaystyle \int_{\Gamma}^{}$ $\displaystyle \Big($ Q(z', z)W(z') - Q(z, z')W(z) $\displaystyle \Big)$ dz'

While this result holds for arbitrary convex functions F(x), the second law for linear kinetic equations is not a consequence of the special definition of the entropy by the log function. Any negative entropy, defined by H(t) = $\left<\vphantom{F \left( p_\infty/p(t) \right), p(t) }\right.$ F $\left(\vphantom{ p_\infty/p(t) }\right.$ p/p(t) $\left.\vphantom{ p_\infty/p(t) }\right)$ , p(t) $\left.\vphantom{F \left( p_\infty/p(t) \right), p(t) }\right>$ is constant in a deterministic system and decreases in a random system.

Lyapunov functions for positive linear evolution problems in *

Lyapunov functions for positive linear evolution problems in $\cal {C}$ ^*