A quantum transmitting Schrödinger-Poisson system
Collaborator: M. Baro,
H.-Chr. Kaiser,
H. Neidhardt,
J. Rehberg
Cooperation with:
A. Jüngel (Johannes Gutenberg-Universität Mainz),
P. Degond, N. Ben Abdallah (Université Paul Sabatier,
Toulouse, France),
V.A. Zagrebnov (Université de la Méditerranée, Aix-Marseille
II and Centre de Physique Théorique, France),
P. Exner (Academy of Sciences of the Czech Republic, Prague)
Supported by: DFG: DFG-Forschungszentrum ``Mathematik für
Schlüsseltechnologien'' (Research Center ``Mathematics for Key
Technologies''), project D4;
``Kopplung von van Roosbroeck- und Schrödinger-Poisson-Systemen mit
Ladungsträgeraustausch'' (Coupling between van Roosbroeck and
Schrödinger-Poisson systems with carrier exchange); DAAD
(PROCOPE): ``Numerics of hybrid models for quantum
semiconductors''
Description:
This project is part of a long-term investigation of quantum
mechanical models for semiconductor nanostructures,
cf.
[2, 9, 10, 11,
12, 13, 14],
and their embedding into macroscopic models, like drift-diffusion and
energy models, cf.
[15]
and p. ![[*]](http://www.wias-berlin.de/misc/icons/crossref.gif) ,
for semiconductor devices,
in particular optoelectronic ones, cf.
[1, 3]
and pp.
,
for semiconductor devices,
in particular optoelectronic ones, cf.
[1, 3]
and pp. ![[*]](http://www.wias-berlin.de/misc/icons/crossref.gif) ,
, ![[*]](http://www.wias-berlin.de/misc/icons/crossref.gif) .
.
We investigate, from a mathematical point of view, a
basic quantum mechanical model for the transport of electrons and
holes in a semiconductor device.
More precisely, our subject is the distribution of electrons and holes
in a device between two reservoirs within a self-consistent electrical
field, thereby taking into account quantum phenomena such as tunneling
and the quantization of energy levels in a quantum well.
These very quantum effects are the active principle of many
nanoelectronic devices: quantum well lasers, resonant tunneling
diodes et cetera, cf., e.g., [17].
We look for stationary states of a quasi-two-dimensional
electron-hole gas
in a semiconductor heterostructure which is
translationally invariant in these two dimensions. Thus, neglecting any
magnetic field induced by the carrier currents, we are dealing with an
essentially one-dimensional physical system.
The transport model
for a single band, electrons
or holes, in a given spatially varying potential v is as follows:
The potential v as well as the material parameters
of the physical system are constant outside a fixed interval (a, b),
cf. [7, 16].
The possible wave functions are given by the generalized solutions of
where
is the single-particle effective-mass Hamiltonian in Ben-Daniel-Duke
form, 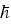 is the reduced Planck constant, m = m(x) > 0 is the
spatially varying effective mass of the particle species under
consideration, and
is the reduced Planck constant, m = m(x) > 0 is the
spatially varying effective mass of the particle species under
consideration, and
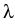 =
= 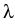 (k) is a dispersion relation, e.g.,
(k) is a dispersion relation, e.g.,
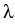
(
k) =
![$\displaystyle \begin{cases}
\frac{\hbar^2k^2}{2m_a}+v_a
\quad&\text{for $k>0$,}
[1ex]
\frac{\hbar^2k^2}{2m_b}+v_b
\quad&\text{for $k<0$;}
\end{cases}$](img91.gif)
ma, mb are the effective masses, and va, vb are the
potentials in the asymptotic regions x < a and x > b, respectively.
If there are no bounded states, then
the particle density u is a composition of the wave functions 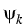 weighted by values of a distribution function f:
weighted by values of a distribution function f:
u(x) = c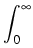 dk f ( dk f (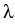 (k) - (k) - 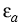 )| )|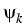 (x)|2 + c (x)|2 + c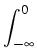 dk f ( dk f (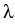 (k) - (k) - 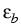 )| )|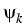 (x)|2, x (x)|2, x 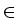 (a, b). (a, b).
|
(2) |
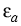 and
and
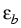 is the quasi-Fermi potential of the
reservoir in the asymptotic region x < a and x > b, respectively, and
c is the two-dimensional density of states.
The distribution function is
is the quasi-Fermi potential of the
reservoir in the asymptotic region x < a and x > b, respectively, and
c is the two-dimensional density of states.
The distribution function is
f (
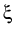
) =
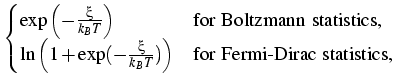
where T is the temperature and kB Boltzmann's constant.
(2) can be written in the following way:
Let
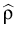 be the multiplication operator on
be the multiplication operator on
 2(
2(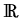 ) induced by the function
) induced by the function
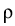 (k) = (k) = 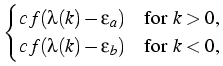
|
(3) |
and let
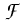 v :
v : 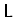 2(
2(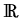 )
)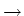
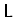 2(
2(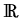 )be the Fourier transform
which diagonalizes the operator Kv on
)be the Fourier transform
which diagonalizes the operator Kv on
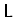 2(
2(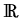 ),
that means
),
that means
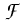 vKv
vKv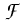 v * =
v * = 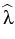 ,where
,where
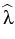 is the maximal multiplication operator induced by
the dispersion relation
is the maximal multiplication operator induced by
the dispersion relation
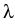 =
= 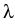 (k).
Then the operator
is a steady-state, that means a self-adjoint, positive operator
on the Hilbert space
(k).
Then the operator
is a steady-state, that means a self-adjoint, positive operator
on the Hilbert space
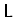 2(
2(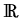 ) which commutes
with Kv.
Moreover, any steady state can be expressed in the form
(4) by means of a function
) which commutes
with Kv.
Moreover, any steady state can be expressed in the form
(4) by means of a function
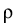 =
= 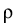 (k).
The particle density u, defined by (2), is the
Radon-Nikodým derivative of the (Lebesgue) absolutely continuous
measure
(a, b)
(k).
The particle density u, defined by (2), is the
Radon-Nikodým derivative of the (Lebesgue) absolutely continuous
measure
(a, b) 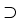
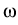
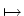 tr
tr 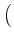
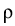 (v)M(
(v)M(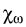 )
)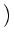 (
M(
(
M(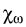 ) denotes the multiplication operator induced by the
characteristic function
) denotes the multiplication operator induced by the
characteristic function
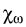 of the set
of the set 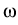 ) that means
for all Lebesgue measurable subsets
) that means
for all Lebesgue measurable subsets 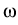 of (a, b).
By replacing the real-valued distribution function (3) by
a generalized distribution function with 2x2-matrix values, this
concept of particle density carries over to the setup we investigate
in this project, cf. [4, Section 5.1].
It should be noted that
the species current density between the reservoirs also can be
expressed in terms of the
of (a, b).
By replacing the real-valued distribution function (3) by
a generalized distribution function with 2x2-matrix values, this
concept of particle density carries over to the setup we investigate
in this project, cf. [4, Section 5.1].
It should be noted that
the species current density between the reservoirs also can be
expressed in terms of the 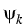 ,
cf. [4, Section 5.2].
,
cf. [4, Section 5.2].
In the asymptotic regions x < a and x > b the generalized
eigenfunctions 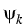 can be written as a superposition of plane
waves. This allows to define boundary conditions at a and b, with
respect to the dispersion relation
can be written as a superposition of plane
waves. This allows to define boundary conditions at a and b, with
respect to the dispersion relation
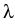 =
= 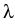 (k), by means of
the quantum transmitting boundary method,
cf.
[7, 16].
The corresponding homogeneous boundary conditions are
(k), by means of
the quantum transmitting boundary method,
cf.
[7, 16].
The corresponding homogeneous boundary conditions are
where
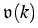 ,
k
,
k 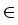
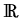 , is the group velocity defined by
, is the group velocity defined by
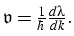 The differential expression (1), together with the boundary
conditions (6), sets up a family of maximal dissipative
operators on the Hilbert space
The differential expression (1), together with the boundary
conditions (6), sets up a family of maximal dissipative
operators on the Hilbert space
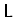 2(a, b). We call this
family, in the style of [16],
the quantum transmitting boundary operator family
(QTB operator family), cf.
[4, Section 2].
The QTB operator family already contains all the information needed to
define, in conjunction with a generalized distribution function
2(a, b). We call this
family, in the style of [16],
the quantum transmitting boundary operator family
(QTB operator family), cf.
[4, Section 2].
The QTB operator family already contains all the information needed to
define, in conjunction with a generalized distribution function
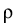 , physical quantities such as the particle density, the current
density, and the scattering matrix.
, physical quantities such as the particle density, the current
density, and the scattering matrix.
The interaction between an electric field and carriers of charge
within a semiconductor device can be modeled by Poisson's equation,
cf. [8]
and the
references cited there:
- 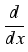 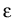 (x) (x)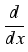 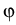 (x) = q (x) = q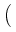 C(x) + C(x) + 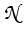 +(v+)(x) - +(v+)(x) - 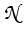 -(v-)(x) -(v-)(x)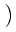 , x , x 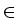 (a, b), (a, b),
|
(7) |
where q denotes the elementary charge, C is the density of ionized
dopants in the semiconductor device,
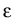 > 0 is the dielectric
permittivity function, and
> 0 is the dielectric
permittivity function, and 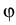 is the electrostatic potential,
v
is the electrostatic potential,
v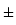 =
=  w
w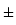
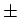 q
q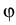 are the potential energies of electrons
(``-'') and holes (``+''), and w-, w+ are the conduction and
valence band offset, respectively.
The quantum transmitting Schrödinger-Poisson system is a Poisson
equation (7) with nonlinear electron and hole density
operators
are the potential energies of electrons
(``-'') and holes (``+''), and w-, w+ are the conduction and
valence band offset, respectively.
The quantum transmitting Schrödinger-Poisson system is a Poisson
equation (7) with nonlinear electron and hole density
operators
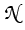 - and
- and
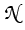 + defined as the map of a
potential v to the density (5) with steady states
+ defined as the map of a
potential v to the density (5) with steady states
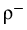 (v) and
(v) and
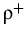 (v), respectively.
In [4, Section 6]
we have demonstrated that the thus defined carrier density operators
are continuous; the corresponding currents are uniformly bounded for
all potentials v.
We have proved that the quantum transmitting
Schrödinger-Poisson system comprising electrons and holes
always admits a solution provided the function inducing the steady
states has reasonable decay properties with increasing energy.
Furthermore, we give a priori estimates for the solutions. The a
priori bounds for the electrostatic potential and the electron and
hole density of solutions are explicit expressions in the data of the
problem.
Ben Abdallah, Degond, and Markowich have investigated a special case
of this model in [6]
and prove the existence of
solutions for the unipolar case.
Unfortunately, the mathematical techniques used in their proof do not
apply to the bipolar case, which we treat in this project.
(v), respectively.
In [4, Section 6]
we have demonstrated that the thus defined carrier density operators
are continuous; the corresponding currents are uniformly bounded for
all potentials v.
We have proved that the quantum transmitting
Schrödinger-Poisson system comprising electrons and holes
always admits a solution provided the function inducing the steady
states has reasonable decay properties with increasing energy.
Furthermore, we give a priori estimates for the solutions. The a
priori bounds for the electrostatic potential and the electron and
hole density of solutions are explicit expressions in the data of the
problem.
Ben Abdallah, Degond, and Markowich have investigated a special case
of this model in [6]
and prove the existence of
solutions for the unipolar case.
Unfortunately, the mathematical techniques used in their proof do not
apply to the bipolar case, which we treat in this project.
The quantum transmitting Schrödinger-Poisson system is
closely related to the dissipative Schrödinger-Poisson
system,
which we have investigated in [5], cf. Annual
Research Report 2002, pp. 26-28. In particular, the dissipative
Schrödinger-Poisson system and the quantum transmitting
Schrödinger-Poisson system coincide for fixed energy,
modulo a unitary transformation.
References:
- U. BANDELOW, H. GAJEWSKI, H.-CHR.
KAISER, Modeling combined effects of carrier injection, photon dynamics
and heating in strained multi-quantum well lasers, in: Physics and
Simulation of Optoelectronic Devices VIII, R.H. Binder, P. Blood,
M. Osinski, eds., vol. 3944, Proceedings of SPIE, SPIE, Bellingham,
WA, August 2000, pp. 301-310.
- U. BANDELOW, H.-CHR. KAISER, TH.
KOPRUCKI, J. REHBERG, Spectral properties of
k . p Schrödinger operators in one space dimension, Numer.
Funct. Anal. Optimization, 21 (2000), pp. 379-409.
- H.-CHR. KAISER, U. BANDELOW, TH.
KOPRUCKI, J. REHBERG,
Modeling and simulation of strained quantum wells in semiconductor
lasers, in: Mathematics--Key Technology for the Future. Joint Projects
Between Universities and Industry, W. Jäger, H.J. Krebs, eds.,
Springer-Verlag, Berlin Heidelberg, 2003, pp. 377-390.
- M. BARO, H.-CHR. KAISER, H.
NEIDHARDT, J. REHBERG, A quantum transmitting
Schrödinger-Poisson system, Rev. Math. Phys., 16
(2004), pp. 281-330.
- , Dissipative Schrödinger-Poisson systems, J.
Math. Phys., 45 (2004), pp. 21-43.
- N. BEN ABDALLAH, P. DEGOND, P.A.
MARKOWICH, On a one-dimensional Schrödinger-Poisson scattering
model, Z. Angew. Math. Phys., 48 (1997), pp. 135-155.
- W. FRENSLEY, Boundary conditions for open quantum systems driven far
from equilibrium, Rev. Mod. Phys., 62 (1990), pp. 745-791.
- H. GAJEWSKI, Analysis und Numerik von Ladungstransport in
Halbleitern (Analysis and numerics of carrier transport in
semiconductors), Mitt. Ges. Angew. Math. Mech., 16 (1993), pp. 35-57.
- H.-CHR. KAISER, H. NEIDHARDT, J.
REHBERG, Density and current of a dissipative Schrödinger
operator, J. Math. Phys., 43 (2002), pp. 5325-5350.
- , Convexity of trace functionals and Schrödinger operators,
WIAS Preprint no. 835, 2003, submitted.
- , Macroscopic current induced boundary conditions for
Schrödinger-type operators, Integral Equations Oper.
Theory, 45 (2003),
pp. 39-63.
- , On one-dimensional dissipative Schrödinger-type operators,
their dilations and eigenfunction expansions, Math. Nachr., 252
(2003), pp. 51-69.
- H.-CHR. KAISER, J. REHBERG, About a
one-dimensional
stationary Schrödinger-Poisson
system with Kohn-Sham potential, Z. Angew.
Math. Phys., 50 (1999), pp. 423-458.
- , About a stationary Schrödinger-Poisson system with
Kohn-Sham potential in a bounded two- or three-dimensional domain,
Nonlinear Anal., Theory Methods Appl., 41 (2000), pp. 33-72.
- ,
About some mathematical questions concerning the embedding of
Schrödinger-Poisson systems into the drift-diffusion model of
semiconductor devices, in: EQUADIFF 99:
International Conference on Differential Equations, Berlin 1999,
B. Fiedler, K.
Gröger, J. Sprekels, eds., vol. 2, World
Scientific, Singapore [u. a.], 2000, pp. 1328-1333.
- C.S. LENT, D.J. KIRKNER, The quantum transmitting
boundary method, J. Appl. Phys., 67 (1990), pp. 6353-6359.
- C. WEISBUCH, B. VINTER, Quantum Semiconductor Structures:
Fundamentals and Applications, Academic Press, Boston, 1991.
LaTeX typesetting by I. Bremer
2004-08-13
![]() ,
for semiconductor devices,
in particular optoelectronic ones, cf.
[1, 3]
and pp.
,
for semiconductor devices,
in particular optoelectronic ones, cf.
[1, 3]
and pp. ![]() ,
, ![]() .
.
![$\displaystyle \begin{cases}
\frac{\hbar^2k^2}{2m_a}+v_a
\quad&\text{for $k>0$,}
[1ex]
\frac{\hbar^2k^2}{2m_b}+v_b
\quad&\text{for $k<0$;}
\end{cases}$](img91.gif)
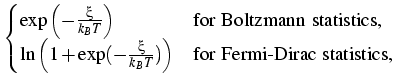
![]() can be written as a superposition of plane
waves. This allows to define boundary conditions at a and b, with
respect to the dispersion relation
can be written as a superposition of plane
waves. This allows to define boundary conditions at a and b, with
respect to the dispersion relation
![]() =
= ![]() (k), by means of
the quantum transmitting boundary method,
cf.
[7, 16].
The corresponding homogeneous boundary conditions are
(k), by means of
the quantum transmitting boundary method,
cf.
[7, 16].
The corresponding homogeneous boundary conditions are