[Next]:  Numerical analysis of complex stochastic models  
 [Up]:  Project descriptions  
 [Previous]:  Statistical data analysis  
 [Contents]   [Index] 

Subsections

Applied mathematical finance

Collaborator: S. Jaschke , A. Kolodko , G.N. Milstein , O. Reiß , J. Schoenmakers , V. Spokoiny , J.-H. Zacharias-Langhans

Cooperation with: P. Annesly (Riskwaters Group, London, UK), H. Föllmer, W. Härdle, U. Küchler, R. Stehle (Humboldt-Universität (HU) zu Berlin), H. Haaf, U. Wystup (Commerzbank AG, Frankfurt am Main), A.W. Heemink (Technical University Delft, The Netherlands), J. Kienitz, S. Schwalm (Reuters AG, Düsseldorf/Paris), K. Sundermann (Postbank AG, Bonn), P. Kloeden (Johann Wolfgang Goethe-Universität Frankfurt am Main), C. März, D. Dunuschat, T. Sauder, T. Valette, S. Wernicke (Bankgesellschaft Berlin AG, Berlin), O. Kurbanmuradov (Physics and Mathematics Research Center, Turkmenian State University, Ashkhabad), M. Schweizer (Technische Universität Berlin/Universität München), G. Stahl (Bundesaufsichtsamt für das Kreditwesen (BAFin) Bonn)

Supported by: BMBF: ``Effiziente Methoden zur Bestimmung von Risikomaßen'' (Efficient methods for valuation of risk measures),
DFG: DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien'' (Research Center ``Mathematics for Key Technologies''); SFB 373 ``Quantifikation und Simulation ökonomischer Prozesse'' (Quantification and simulation of economic processes),
Bankgesellschaft Berlin AG

Description:

The project Applied mathematical finance of the research group ``Stochastic Algorithms and Nonparametric Statistics'' is concerned with the stochastic modeling of financial data, the valuation of derivative instruments (options), and risk management for banks. The implementation of the developed models and their application in practice is done in cooperation with financial institutions.

Since the Basel Committee's proposal for ``An internal model-based approach to market risk capital requirements'' (1995) was implemented in national laws, banks have been allowed to use internal models for estimating their market risk and have been able to compete in the innovation of risk management methodology. Since all banks are required to hold adequate capital reserves with regard to their outstanding risks, there has been a tremendous demand for risk management solutions. A similar ``internal ratings-based approach'' is planned for the controlling of credit risk in the ``Basel II'' process, which is due to be implemented in national laws by 2006. Meanwhile, credit derivatives play an important role as vehicle for banks to transform credit risk into de jure market risk and to potentially lower the required reserves. Such problems of risk measurement and risk modeling are the subject of the research on ``Mathematical methods for risk management''. This research is supported by the BMBF project ``Efficient methods for valuation of risk measures'', which continued in 2002 in cooperation with and with support of Bankgesellschaft Berlin AG. Problems of both market and credit risk from the viewpoint of supervisory authorities are being worked on in cooperation with the BAFin.

The valuation of financial derivatives involves non-trivial mathematical problems in martingale theory, stochastic differential equations, and partial differential equations. While its main principles are established (Harrison, Pliska 1981), many numerical problems remain, such as the numerical valuation of American options and the valuation of financial derivatives involving the term structure of interest rates (LIBOR models) or volatility surfaces. By the continuing innovations in the financial industry new problems arise again and again. In the progressing research on interest rate (LIBOR) modeling and calibration [19, 32, 33] a crucial stability problem has been uncovered with respect to direct least-squares calibration of LIBOR models. As a solution a stabilized procedure is proposed in [31] and was presented at Risk Europe 2002 (Paris) and at Risk Quantitative Finance 2002 (London). On this subject a consulting contract with Reuters Financial Software (Paris) has been set up.

The project ``Applied mathematical finance'' took part in the formation of the DFG Research Center ``Mathematics for Key Technologies''.

1. Mathematical methods for risk management

(S. Jaschke, O. Reiß, J. Schoenmakers, V. Spokoiny, J.-H. Zacharias-Langhans).

Although the basic principles of the evaluation of market risks are now more or less settled, in practice many thorny statistical and numerical issues remain to be solved. Specifically the industry standard, the approximation of portfolio risk by the so-called ``delta-gamma normal'' approach, can be criticized because of the quadratic loss approximation and the Gaussian assumptions. Further, in the context of the ``Basel II'' consultations fundamental questions arise in the area of Credit Risk Modeling.

One of the problems that arose in the consulting with Bankgesellschaft Berlin led to a study of the Cornish-Fisher approximation in the context of delta-gamma normal approximations. This study was enhanced and completed [14]. The analysis shows a series of qualitative shortcomings of the method, while its quantitative behavior is satisfactory in specific situations. Regarding Bankgesellschaft's use of the Cornish-Fisher approximation, it is concluded that the method is a competitive technique if the portfolio distribution is relatively close to normal. It achieves a sufficient accuracy potentially faster than the other numerical techniques (mainly Fourier inversion, saddle-point methods, and partial Monte Carlo) over a certain range of practical cases. One should beware, however, of the many qualitative shortcomings and its bad worst-case behavior. If one takes the worst-case view and cares about the corner cases--as we believe one should in the field of risk management--the potential errors from the quadratic approximation are much larger than the errors from the Cornish-Fisher expansion. Hence a full-valuation Monte Carlo technique should be used anyway to frequently check the suitability of the quadratic approximation. This will also take care of the ``bad'' cases for the Cornish-Fisher approximation.


Fig. 1: A comparison of the improved FFT method and the plain FFT method
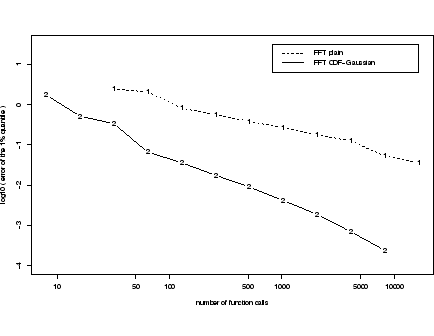
\ProjektEPSbildNocap {10 cm}{FFT-F-N-versus-plain.eps} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}

In the context of delta-gamma approximations, the study of Fourier inversion techniques was continued. [15] is a worst-case error analysis of non-adaptive, FFT-based approximations to the Fourier inversion integral of the cumulative distribution function (minus the Gaussian CDF) in this context. The error analysis allows to optimize certain parameters to achieve the asymptotically optimal rate of convergence. Empirical evidence is presented to show how the results of the error analysis can improve the performance over a plain-vanilla FFT inversion.

K=26 evaluations of the characteristic function suffice to ensure an accuracy of one digit in the approximation of the 1% quantile over a sample of one- and two-factor cases. K=29 function evaluations are needed for two digits accuracy. In comparison, a straightforward (non-optimized) FFT inversion of the probability density needs about 213 function calls to achieve one digit accuracy (see Figure 1).

This error analysis required the characterization of the tail behavior of the probability distribution of quadratic forms of Gaussian vectors, which is the subject of [16]. It provides a complete analysis of the tail behavior of this class of distributions and solves a problem that remained open in [15].

An overview of the Fourier inversion, Monte Carlo simulation and Cornish-Fisher expansion in the context of delta-gamma normal models is given by [18].

In joint work with Gerhard Stahl (BAFin Bonn) and Richard Stehle (HU Berlin), an empirical analysis of the forecast quality of VaR models of the 13 German banks that use internal models for regulatory market risk capital is performed. The goal of the analysis is to answer the following questions:

In preparation of the lecture ``Risk Management for Financial Institutions'' (Risikomanagement für Banken), given by S. Jaschke in the winter semester 2001/2002, an extensive review of the general literature on the subject was done. The practical implementation of an enterprise-wide risk management system needs an understanding of the economic, statistical, numerical, social, and information technology aspects of the problem. The insights gained from the study of the general literature allow to assess not only the inner-mathematical relevancy, but also the practical relevancy of new ideas and open problems. The lecture notes are available from http://www.cofi.de/risk-lecture.html.

In the context of the BMBF project ``Efficient methods for the valuation of risk measures'', which is treated in cooperation with the Bankgesellschaft Berlin AG, we focus on the problem of estimating the market risk of large portfolios by the Monte Carlo method. Our first goal is the efficient estimation of the above-mentioned quantile-VaR, which is from a practical point of view the most important risk measure. The results obtained for the VaR shall subsequently be used for estimating more complex risk measures, like the conditional Value at Risk and related quantities.

There are only two possibilities for accelerating the convergence of the Monte Carlo procedure. First, to reduce the number of steps (i.e. portfolio evaluations) necessary for reaching a given error level by variance reduction (important sampling, stratified sampling, etc.). Second, to reduce the time needed for a single step, by using fast algorithms for pricing the portfolio's components. The latter possibility is described below. Concerning the first point, a well-known ([9]) technique for variance reduction, which is based on the delta-gamma normal approximation has been implemented. By construction, this method fails to reduce variance, if the portfolio is very different from its delta-gamma approximation, which may happen for example if the portfolio is hedged. Therefore, we develop an adaptive sampling algorithm, where a Markov chain of Metropolis-Hastings type is used to create scenarios according to any given profit and loss distribution. Because of intrinsic difficulties, like the lack of global information, it is not clear whether this procedure can be used as a method for variance reduction. On the other hand, it allows for a detailed analysis of critical scenarios, giving for example information about the implied correlation structure, and the risk, inherent in changes of the correlation structure, the underlying processes are originally supposed to follow. Even small fluctuations of the correlation can cause huge losses, as the 1998 crash of hedge fund LTCM has impressively shown. Part of our work was also the programming of a Java-based graphical interface, which allows to dynamically value ``real-life'' portfolios. It organizes dependent market data and supplies the mathematical structures for the developed numerical routines, and also monitors and exploits statically the outcome of the Monte Carlo scheme during its run. Most of the numerical routines developed in context with this project are used in this program, which is actually running on a test level in the bank.

In cooperation with and supported by the Bankgesellschaft Berlin AG we worked on the efficient valuation of complex financial instruments, for example American options and convertible bonds. By some modifications of the standard binomial tree model, we could significantly increase speed and accuracy of the algorithm by reducing the computational effort of order N2 to N1.5, where N is the number of time steps used. Especially in context with high-accuracy calculations, which are necessary at the trading level for a stable treatment of sensitivities, the effect of this improvement becomes significant. So the use of very large numbers of time steps is now allowed, which is far beyond typical numbers used in comparative studies [1, 4]. Another modification, concerning the position of the tree nodes and which is interesting, for example, in view of the applicability of Richardson extrapolation techniques, led to an interpolation problem which could partially be solved, resulting in a smoothed convergence behavior of the algorithm. For standard American options, this method gives results comparable to the BBSR model described in [4]. By further improving the interpolation procedure, it seems to be possible to get even better results. A completely different algorithm, based on the Fast Fourier Transform, was also developed and analyzed. It was shown to be useful for the valuation of Bermudan-type options, but also for the standard American call, on an underlying paying of a large number of dividends, as for example index options. Another problem tackled in this context was how to incorporate credit risk in the valuation of instruments like, e.g., convertible bonds or ASCOTs. We implemented three distinct models, enabling therefore our cooperation partner to switch to the most adapted model for the specific situation.

The analysis of the delta-gamma normal algorithm to determine the Value at Risk has made substantial progress. In order to deal with rank deficient or perturbed correlation matrices a generalized Cholesky decomposition algorithm was developed [26]. To obtain the distribution of the profit-and-loss distribution, adapted Fourier inversion algorithms have been designed, and the use of the double exponential integration has been analyzed. Error bounds concerning the decay properties of the involved functions in x-space as well as in Fourier space have been developed.

One industrial standard to handle credit risk is CreditRisk+, which was developed by Credit Suisse First Boston in 1997. Based on the improving techniques we developed in the context of the delta-gamma normal method, this model has been analyzed and it turned out that similar Fourier inversion techniques can improve this model, too. Furthermore, generalizations of this model have been introduced, and an incorporation of credit risk and market risk within such a generalized framework has been established [27]. The research on this topic is related to the research topic E5 ``Statistical and numerical methods in modeling and valuation of financial derivatives and portfolio risk'' of the DFG Research Center ``Mathematics for Key Technologies''.

2. Interest rate (LIBOR) modeling, calibration and pricing of non-standard derivatives

(A. Kolodko, G.N. Milstein, O. Reiß, J.G.M. Schoenmakers).

A very popular interest rate model is the LIBOR market model [3, 13, 24] which is given by

$\displaystyle{}dL_i=-\sum_{j=i+1}^{n-1}\frac{\delta_jL_iL_j\, \gamma_i\cdot\gamma_j}{1+\delta_jL_j}\,dt +L_i\,\gamma_i\cdot dW^{(n)},$      (1)
where the LIBOR/EurIBOR processes Li are defined in [t0,Ti] with $\delta_i=T_{i+1}-T_i$ being day count fractions and $\gamma_i$ = $(\gamma_{i,1},\ldots,\gamma_{i,d})$ deterministic volatility functions. Further, $(W^{(n)}(t)\mid t_0\leq$ $t\leq T_{n-1})$ is a d-dimensional Wiener process under the so-called terminal measure $\mbox{$\rm{I\!P}$}_n.$

Calibration of a LIBOR market model to liquidly traded instruments such as caps and swaptions has been a challenging problem for several years. In particular, calibration methods which avoid the use of historical data are very desirable, both from a practical and a more fundamental point of view. Previously we derived, on a conceptual basis, a variety of parsimonious correlation structures suitable for implementation in the LIBOR/EurIBOR market model (1). Here is an example of a realistic two-parametric structure,

\begin{eqnarray*} \rho_{ij}&=&\exp\left[-\frac{\vert j-i\vert}{m-1} \left(-\ln\r... ... \right)\right],\nonumber\ &&\eta\gt,\ 0<\eta<-\ln\rho_{\infty}.\end{eqnarray*}

These correlation structures combined with suitable parametrizations of the volatility norms $\vert\gamma_i\vert$ form the corner-stones of our calibration procedure. However, we detected an intrinsic stability problem in joint calibration of a multi-factor LIBOR market model with time-dependent volatility norms using the standard least-squares approach. This has led to incorporation of a new concept, the so-called ``Market Swaption Formula'' which is an intuition-based approximation of swaptions, in the objective function of the calibration routine [31]. By the method described in [31] stable calibration of a LIBOR market model to a whole system of caplet and swaption volatilities turns out to be feasible with only four parameters volatilities. Most of all this calibration remains stable even if the quality of the market data is less. Further, a refined approximation procedure for swaption prices has been derived. This method takes into account the issue of differently settled caps and swaptions and improves upon the method of Jäckel and Rebonato (2001). The respective algorithms are implemented as Excel add-ins and are currently used for consulting purposes (Reuters Financial Software).

In a more economically motivated study we previously developed the concept of dealing with assets and interest rates in a unified model which is completely specified by the assets alone. This allowed for endogenous derivations of dynamic relations between assets and interest rates from global structural assumptions (homogeneity and some spherical symmetry) on the market. In particular, with respect to a rather general well-structured model we derived a relationship between the so-called spherical index and the short rate which may be regarded as an extension of earlier results and has the following interpretation:

  • If R(t0,T)>r0, hence the yield curve goes up (most usual), then the local correlation of short rate r and (spherical) index I is negative.
  • If R(t0,T)<r0, hence the yield curve goes down, then the local correlation of short rate r and (spherical) index I is positive.
Further, when the spherical index satisfied the assumptions of the Capital Asset Pricing Model we obtained that
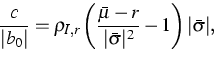\begin{displaymath} \frac{c}{\vert b_0\vert} = \rho_{I,r} \left( \frac{\bar{\mu}-r}{\vert\bar{\sigma}\vert^2}-1 \right) \vert\bar{\sigma}\vert ,\end{displaymath} (2)
where c is the objective drift, and b0 the volatility of the short rate, $\bar{\mu}$ the objective drift and $\bar{\sigma}$ the volatility of the stock index, and $\rho_{I,r}$ the correlation between short rate and index. As a consequence, with respect to the new economic pointer $q:=(\bar{\mu}-r)/\vert\bar{\sigma}\vert^2,$ the market can be found in the following states:
Table 1: Effect of q and the short yield on the objective (real) short rate drift c
size of q short yield c (real drift)
>1 down +
>1 up -
=1 ? 0
<1 down -
<1 up +

The above research is currently subject of empirical study and was presented at the Bachelier Congress 2002 [28].

For computing of option sensitivities we developed in [29] an analytical method and in [21] a Monte Carlo approach. The methods in [21] have been extended to determine the price and hedge of certain American options [20]. In this research we utilize more sophisticated algorithms for the simulation of stochastic differential equations in the neighborhood of a boundary [23].

The research on Bermudan-style interest rate derivatives has been placed in the context of the DFG Research Center ``Mathematics for Key Technologies''. In particular, we are currently investigating a connection of these types of derivatives with a method proposed by Rogers [30].


References:

  1. F. AITSAHLIA, P. CARR, American options: A comparison of numerical methods, in: Numerical Methods in Finance, L.C.G. Rogers, D. Talay, eds., Cambridge University Press, 1997, pp. 67-87.
  2. P. ARTZNER, F. DELBAEN, J.M. EBER, D. HEATH, Coherent measures of risk, Math. Finance, 9 (1998), pp. 203-228.
  3. A. BRACE, D. GATAREK, M. MUSIELA, The market model of interest rate dynamics, Math. Finance, 7 (1997), pp. 127-155.
  4. M. BROADIE, J. DETEMPLE, Recent advances in numerical methods for pricing derivative securities, in: Numerical Methods in Finance, L.C.G. Rogers, D. Talay, eds., Cambridge University Press, 1997, pp. 43-66.
  5. P. EMBRECHTS, C. KLÜPPELBERG, T. MIKOSCH, Modelling Extremal Events, Springer, Berlin, 1997.
  6. P. EMBRECHTS, A. MCNEIL, D. STRAUMANN, Correlation: Pitfalls and alternatives, RISK Magazine, May 1999, pp. 69-71.
  7. J. FRANKE, W. HÄRDLE, G. STAHL, Measuring risk in complex stochastic systems, Lecture Notes in Statist., 147, Springer, New York, 2000.
  8. P. GLASSERMAN, X. ZHAO, Arbitrage-free discretization of lognormal forward Libor and swap rate models, Finance and Stochastics, 4 (2000), pp. 35-68.
  9. P. GLASSERMAN, P. HEIDELBERGER, P. SHAHABUDDIN, Importance sampling and stratification for Value-at-Risk, in: Computational Finance 1999, Y.S. Abu-Mostafa, B. Le Baron, A.W. Lo, A.S. Weigend, eds., MIT Press, , Cambridge, Mass., 2000, pp. 7-24.
  10. A. GOMBANI, S. JASCHKE, W. RUNGGALDIER, A filtered no arbitrage model for term structures from noisy data, WIAS Preprint no. 759, 2002.
  11. A. GOMBANI, W. RUNGGALDIER, A filtering approach to pricing in multifactor term structure models , Internat. J. Theoret. Appl. Finance, 4 (2001), pp. 303-320.
  12. W. HÄRDLE, H. HERWARTZ, V. SPOKOINY, Time inhomogeneous multiple volatility modelling, Discussion Papers of Interdisciplinary Research no. 7, Humboldt-Universität zu Berlin, SFB 373, 2001.
  13. F. JAMSHIDIAN, LIBOR and swap market models and measures, Finance and Stochastics, 1 (1997), pp. 293-330.
  14. S. JASCHKE, The Cornish-Fisher expansion in the context of delta-gamma-normal approximations, Journal of Risk, 4 (2002), pp. 33-52.
  15. \dito , Error analysis of quantile-approximations using Fourier inversion in the context of delta-gamma normal models, GARP Risk Review, 6 (2002), pp. 28-33.
  16. S. JASCHKE, C. KLÜPPELBERG, A. LINDNER, Asymptotic behavior of tails and quantiles of quadratic forms of Gaussian vectors, Discussion Paper no. 280, Technische Universität München, 2002.
  17. S. JASCHKE, U. KÜCHLER, Coherent risk measures and good-deal bounds, Finance and Stochastics, 5 (2001), pp. 181-200.
  18. S. JASCHKE, Y. YIANG, Approximating value at risk in conditional Gaussian models, in: Applied Quantitative Finance, W. Härdle, T. Kleinow, G. Stahl, eds., Springer, 2002, pp. 3-33.
  19. O. KURBANMURADOV, K.K. SABELFELD, J.G.M. SCHOENMAKERS, Lognormal approximations to LIBOR market models, J. Computational Finance, 6 (2002), pp. 69-100.
  20. G.N. MILSTEIN, O. REISS, J.G.M. SCHOENMAKERS, Monte Carlo methods for pricing and hedging American options, working paper, 2002.
  21. G.N. MILSTEIN, J.G.M. SCHOENMAKERS, Monte Carlo construction of hedging strategies against multi-asset European claims, Stochastics Stochastics Rep., 73 (2002), pp. 125-157.
  22. G.N. MILSTEIN, J.G.M. SCHOENMAKERS, V. SPOKOINY, Transition density estimation for stochastic differential equations via forward-reverse representations, WIAS Preprint no. 680, 2001.
  23. G.N. MILSTEIN, M.V. TRETYAKOV, Simulation of a space-time bounded diffusion, Ann. Appl. Probab., 9 (1999), pp. 732-779.
  24. K.R. MILTERSEN, K. SANDMANN, D. SONDERMANN, Closed-form solutions for term structure derivatives with lognormal interest rates, J. Finance, 52 (1997), pp. 409-430.
  25. R.B. NELSON, An Introduction to Copulas, Springer, New York, 1999.
  26. O. REISS, A generalized non-square Cholesky decomposition algorithm with applications to finance, WIAS Preprint no. 760, 2002.
  27. \dito , Fourier inversion algorithms for generalized CreditRisk+ models and an extension to incorporate market risk, working paper, 2002.
  28. O. REISS, J.G.M. SCHOENMAKERS, M. SCHWEIZER, Endogenous interest rate dynamics in asset markets, WIAS Preprint no. 652, 2001.
  29. O. REISS, U. WYSTUP, Computing option price sensitivities using homogeneity and other tricks, in: Foreign Exchange Risk: Models, Instruments and Strategies, Risk Books, London, 2002, pp. 127-142.
  30. L.C.G. ROGERS, Monte Carlo valuation of American options, Math. Finance, 12 (2002), pp. 271-286.
  31. J.G.M. SCHOENMAKERS, Calibration of LIBOR models to caps and swaptions: A way around intrinsic instabilities via parsimonious structures and a collateral market criterion, WIAS Preprint no. 740, 2002.
  32. J.G.M. SCHOENMAKERS, B. COFFEY, LIBOR rate models, related derivatives and model calibration, WIAS Preprint no. 480, 1999.
  33. \dito , Stable implied calibration of a multi-factor LIBOR model via a semi-parametric correlation structure, WIAS Preprint no. 611, 2000.
  34. J.G.M. SCHOENMAKERS, A.W. HEEMINK, K. PONNAMBALAM, P.E. KLOEDEN, Variance reduction for Monte Carlo simulation of stochastic environmental models, Appl. Math. Modelling, 26 (2002), pp. 785-795.


 [Next]:  Numerical analysis of complex stochastic models  
 [Up]:  Project descriptions  
 [Previous]:  Statistical data analysis  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
5/16/2003