|
|
|
[Contents] | [Index] |
(FG 1)
Supported by: DFG: Priority Program ``Analysis, Modellbildung und Simulation von Mehrskalenproblemen'' (Analysis, modeling and simulation of multiscale problems)
Description:
This is a joint project of Dreyer/Sprekels. In the last period two questions were posed and answered:
Regarding the first question, we have shown that the answer is affirmative only for a special class of microscopic initial conditions, namely those that can be prepared macroscopically.
Regarding the second question, we have studied simple cases, where the microscopic observables only depend on time but not on the particle index. A well-known example is the oscillator motion of the atomic chain, which can be found in [1].
Let ![]() be the microscopic time.
be the microscopic time. ![]() denotes a
microscopic observable that depends continuously on the microscopic
variable
denotes a
microscopic observable that depends continuously on the microscopic
variable ![]() with
with ![]() . The
macroscopic time is defined by
. The
macroscopic time is defined by ![]() where
where ![]() is a small positive parameter, and the macroscopic limit can be
established for
is a small positive parameter, and the macroscopic limit can be
established for ![]() . To this end we define
. To this end we define
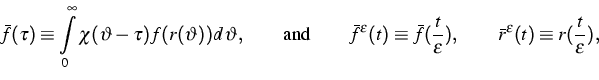 |
(1) |
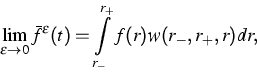 |
(2) |
A second simple example serves to illustrate the suitable mathematics of the
macroscopic limit. We consider the following Newtonian system that
contains the small parameter ![]() :
:
The macroscopic time is defined by ![]() , so that the force f
varies only on the macroscopic scale, while the variable Q oscillates on
the microscopic scale. Fig. 1 shows a typical example:
There is a rapid oscillation for small
, so that the force f
varies only on the macroscopic scale, while the variable Q oscillates on
the microscopic scale. Fig. 1 shows a typical example:
There is a rapid oscillation for small ![]() from the macroscopic
viewpoint.
from the macroscopic
viewpoint.
For fixed ![]() and fixed macroscopic time tfinal there
exists, within the time interval
and fixed macroscopic time tfinal there
exists, within the time interval ![]() , a solution
, a solution ![]() of
(3) that we rescale according to
of
(3) that we rescale according to
| (4) |
The most important observable is the energy e, which is given by
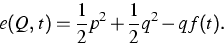 |
(5) |
The functions ![]() and
and
![]() converge to Young measures
converge to Young measures ![]() and
and ![]() , respectively. Precisely we write
, respectively. Precisely we write ![]() and
and
![]() although
although ![]() and
and ![]() are no functions but
Young measures. The Young measures
are no functions but
Young measures. The Young measures ![]() and
and ![]() are
completely determined by the following properties
are
completely determined by the following properties
![\begin{displaymath}
{\mathrm{div}}_{Q}\,\Big(\mu (t,\,Q)\cdot \lbrack A(Q)-{\Big(
\begin{array}
{c}
{0} \
{f(t)}\end{array}\Big)}]\Big)=0.\end{displaymath}](../2001/img568.gif) |
(6) |
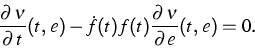
References:
|
|
|
[Contents] | [Index] |