Existenz und Optimierung nichtglatter mechanischer Strukturen

[Next]:

Forschungsgruppe Dynamische Systeme

[Up]:

Projektbeschreibungen

[Previous]:

Mathematische Modellierung von Hysteresephänomenen

[Contents]

[Index]

Existenz und Optimierung nichtglatter mechanischer Strukturen

Bearbeiter: J. Sprekels , D. Tiba

Kooperation: A. Ignat (Universität Iasi, Rumänien)

Beschreibung der Forschungsarbeit: Ziel der Forschungen ist es, die elastische Deformation gekrümmter mechanischer Strukturen unter möglichst geringen Glattheitsanforderungen zu bestimmen. Dazu wurden im Berichtszeitraum Bögen, gekrümmte Stäbe und spezielle Schalenmodelle untersucht. Weitere Resultate zu Platten und Variationsungleichungen finden sich in [9] und [10].

a) Bögen.

Die Untersuchungen befassten sich mit der Modellierung der Deformation eines beidseitig eingespannten Bogens der Dicke $\,\sqrt{\varepsilon}\,$ , der durch eine Kurve $\,\varphi: [0,1]\to \IR^2\,$ beschrieben wird. Sind $\,(f_1,f_2)\in (L^2(0,1))^2\,$ die am Bogen angreifende Kraft und $\,c\,$ die Krümmung des Bogens, so führt (in lokalen Koordinaten) das Kirchhoff-Love-Modell auf die Variationsaufgabe

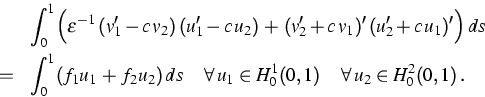
$\begin{eqnarray} &&\int_0^1\Bigl(\varepsilon^{-1}\,(v_1'-c\,v_2)\,(u_1'-c\,u_2) ... ...uad\forall\,u_1\in H^1_0 (0,1)\,\quad\forall\,u_2\in H^2_0(0,1)\,.\end{eqnarray}$

Die Unbekannten $\,v_1\,,\,v_2\,$ stellen dabei die tangentiale bzw. normale Verschiebung des Bogens dar.

Damit (1) sinnvoll ist, wurde bisher in der Literatur (vgl. z. B. [1], [2]) $\,c\in W^{1,\infty}(0,1)\,$ , d. h. $\,\varphi \in (W^{3, \infty} (0, 1))^2\,$ , vorausgesetzt, wodurch praktisch relevante Fälle wie z. B. gothische Bögen ausgeschlossen sind. Zur Überwindung dieser Einschränkung wurde eine neue variationelle Formulierung hergeleitet, die auf Methoden der optimalen Steuerung beruht und auch für den Fall $\,\varphi \in (W^{1, \infty} (0, 1))^2\,$ gültig ist.

Seien dazu $\,g_1 := \varepsilon\, l\,$ und $\,g_2\,$ die eindeutige Lösung von $\,- g_2'' = h\,$ in $\,(0, 1)\,,\, g_2 (0) = g_2 (1) = 0\,$ , wobei sich $\,l\,$ und $\,h\,$ aus der Anfangswertaufgabe

$\begin{displaymath} -\,l'\,-\,c\, h\,=\,f_1\,, \quad c\, l\,-\,h'\,=\,f_2\mbox{ in } (0, 1)\,, \quad l (0)\,=\,h (0)\,=\,0\end{displaymath}$

bestimmen. Wir betrachten dann das unrestringierte Steuerungsproblem:

Finde $\,(u,z;v_1,v_2)\in L^2(0,1)\times H^1_0(0,1)\times H^1_0(0,1)\times H^1_0(0,1)\,$ mit (P)

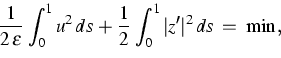
$\begin{displaymath} \frac{1}{2\,\varepsilon}\,\int_0^1u^2\,ds \,+\,\frac{1}{2}\,\int_0^1\vert z'\vert^2\,ds \,\,=\,\,\min\,,\end{displaymath}$

unter der Zustandsgleichung

$\begin{displaymath} c\,v_1+v_2'=z+g_2\,,\quad v_1'-c\,v_2=u+g_1\,,\quad\mbox{in }\, (0,1)\,,\quad v_1(0)=v_2(0)=0\end{displaymath}$

und der Endbedingung

$\begin{displaymath} v_1(1)=v_2(1)=0\,.\end{displaymath}$

Es lässt sich zeigen, dass im Falle $\,c\in W^{1,\infty}(0,1)\,$ für jede Lösung $\,(u,z;v_1,v_2)\,$ von (P) gilt, dass $\,(v_1,v_2)\,$ Lösung von (1) ist und umgekehrt.

Es stellt sich nun heraus, dass das zu (P) duale Problem endlich-dimensional ist und eine vollständige Lösung zulässt. Hieraus erhält man dann sogar explizite Lösungen für die Deformation Lipschitz-stetiger Bögen.

Ferner ergibt sich Folgendes: Schreibt man die notwendigen Optimalitätsbedingungen für (P) (oder für das duale Problem) in Form des Pontryagin'schen Maximum-Prinzips, so erhält man eine spezielle Dekomposition von (1) in ein System von Differentialgleichungen erster Ordnung mit Zweipunkt-Randbedingungen. In dieser Hinsicht stellt der neue Ansatz eine Fortsetzung der von Sprekels und Tiba (vgl. [5, 6, 7]) entwickelten Ideen für Platten und Stäbe dar.

Als weitere Aufgabenstellungen wurden Probleme der Shape-Optimierung für (1) untersucht. Hierbei sind $\,\varphi\,$ (oder c) so zu bestimmen, dass für ein gegebenes Kräftepaar $\,(f_1,f_2)\,$ die resultierende Deformation bestimmte gewünschte Eigenschaften besitzt. Ein typisches Beispiel ist es, die Deformation $\,v_2\,$ in Normalenrichtung im Sinne der $\,L^2(0,1)\,$ -Norm zu minimieren. Es ist im Berichtszeitraum gelungen, die Existenz einer Lösung dieses nichtkonvexen Optimierungsproblems für Lipschitz-stetige Bögen nachzuweisen und die notwendigen Optimalitätsbedingungen erster Ordnung herzuleiten.

Die theoretischen Resultate und die Ergebnisse umfangreicher numerischer Tests sind in [3] und [8] dokumentiert.

b) Gekrümmte Stäbe.

Als weitere Aufgabenstellung wurde im Berichtszeitraum die elastische Deformation dreidimensionaler gekrümmter Stäbe, die eine nichtkonstante Dicke und möglicherweise mehrfach zusammenhängende Querschnitte besitzen, untersucht. Dabei wurde die geometrische Annahme gemacht, dass transversale Schnitte nach Deformation eben bleiben (Scherung und Torsion der Schnitte sind möglich).

Ziel der Untersuchung war wiederum, mit möglichst geringen Glattheitsvoraussetzungen auszukommen. Es gelang dabei, eine weitgehende Theorie für den Fall herzuleiten, dass die Kurve der Schwerpunkte des Stabes eine Parametrisierung $\,\varphi \in (W^{2, \infty})^3\,$ besitzt. Man erhält dabei eine variationelle Formulierung mit einer Bilinearform, die einer Randwertaufgabe für ein lineares System von neun gewöhnlichen Differentialgleichungen entspricht.

Die Glattheitsbedingung $\,\varphi \in (W^{2, \infty})^3\,$ ist schwächer als die in der Literatur üblichen und erlaubt es insbesondere, wichtige neue Optimierungsaufgaben für gekrümmte Stäbe mit Zustandsrestriktionen zu erfassen, die mit der bisherigen Theorie nicht behandelt werden konnten. Entscheidend für diese Fortschritte war dabei die Idee, anstelle des klassischen Frenet'schen andere lokale Koordinatensysteme zur geometrischen Beschreibung der Stäbe zu verwenden. Diese neuen lokalen Koordinatensysteme erwiesen sich auch bei der numerischen Lösung des Problems als sehr vorteilhaft.

Die theoretischen Resultate und die Ergebnisse umfangreicher numerischer Tests sind in der Arbeit [4] dokumentiert.

c) Schalen.

Ziel der Untersuchungen ist es, die für gekrümmte Bögen und Stäbe erzielten Resultate auf allgemeine Schalenmodelle auszudehnen. Als erste Problemklasse wurde dabei im Berichtszeitraum eine verallgemeinerte Version des Naghdi-Modells hergeleitet und für die entsprechenden Modellgleichungen (ein variationelles System, das einer linearen Randwertaufgabe für ein System von sechs linearen partiellen Differentialgleichungen entspricht) Existenz und Eindeutigkeit bewiesen.

Die aus der Literatur bekannten Glattheitsvoraussetzungen, nämlich dass die Mittelfläche der Schale oder die Kurve der Schwerpunkte zu $\,C^3\,$ gehören müssen, konnten wiederum erheblich abgeschwächt werden: Es gelang der Nachweis, dass stückweise C²-Glattheit genügt.

Die entsprechenden theoretischen Resultate sind in der Arbeit [11] zusammengefasst.

Projektliteratur:

D. CHENAIS, J.-C. PAUMIER, On the locking phenomenon for a class of elliptic problems, Numer. Math., 67 (1994), pp. 427-440.
PH. CIARLET, The Finite Element Method for Elliptic Problems, North-Holland, Amsterdam, 1978.
A. IGNAT, J. SPREKELS, D. TIBA, Analysis and optimization of nonsmooth arches, erscheint in: SIAM J. Control Optim.
$\dito$ , A model of a general elastic curved rod , WIAS-Preprint No. 613, 2000, eingereicht.
J. SPREKELS, D. TIBA, A duality-type method for the design of beams , Adv. Math. Sci. Appl., 9 (1999), pp. 89-102.
$\dito$ ,On the approximation and optimization of fourth order elliptic problems, in: Optimal control of partial differential equations (K.-H. Hoffmann et al., Hrsg.), Internat. Ser. Numer. Math., 133, Birkhäuser, Basel, 1999, pp. 277-286.
$\dito$ ,A duality approach in the optimization of beams and plates , SIAM J. Control Optim., 37 (1998/99), pp. 486-501.
$\dito$ ,Sur les arches lipschitziennes, C. R. Acad. Sci. Paris Sér. I Math., 331 (2000), pp. 179-184.
$\dito$ ,Control variational methods for differential equations , WIAS-Preprint No. 610, 2000, eingereicht.
$\dito$ ,Optimization of clamped plates with discontinuous thickness, in Vorbereitung.
$\dito$ ,An analytic approach to generalized Naghdi shell models, in Vorbereitung.