![\begin{eqnarray*}
\frac{\partial n^E(t,x) }{\partial t}+V(t,x)\cdot\nabla_xn^E(t...
...E(t,x)\right)+F(x,t);\quad
n^E(0,x)=0;\quad x\in R^3;\;t\in[0,T].\end{eqnarray*}](../../1998/html/images/img306.gif){kind=small}
|
|
|
[Contents] | [Index] |
Bearbeiter: K. Sabelfeld
Kooperation: S. Orszag (Princeton University, USA), Timo Vesala (Universität Helsinki), P. K. Yeung (Georgian Institute of Technology, USA), O. Kurbanmuradov (Physikalisch-Technisches Institut, Turkmenische Akademie der Wissenschaften, Aschchabad), A. Levykin (Rechenzentrum und Institut für Mathematische Geophysik, Russische Akademie der Wissenschaften, Novosibirsk)
Förderung: EU (INTAS-Projekt) und Nato
Beschreibung der Forschungsarbeit:
Die Entwicklung von mathematischen und insbesondere von stochastischen Modellen des turbulenten Transports von koagulierenden Partikeln ist von großer Bedeutung, weil die Wahrscheinlichkeitstheorie eine natürliche Beschreibung für Mischungen und Reaktionen von kleinen Partikeln in turbulenten Strömungen liefert [1], [3]. Deshalb stellt die Untersuchung des Transportes von koagulierenden Aerosol-Partikeln in einer realistischen Umwelt, wie einer turbulenten Atmosphäre, einen Schwerpunkt dar.
Solche Medien sind charakterisiert durch hohe Fluktuationen der physikalischen Felder. Hierbei ändern sich die zeitlichen und räumlichen Maßstäbe enorm. Dies ist die Ursache aller Schwierigkeiten bei der Benutzung konventioneller deterministischer Methoden, die auf der halbempirischen Gleichung des turbulenten Transports basieren. Deshalb ist die stochastische Betrachtungsweise, die die Natur der Fluktuationen effektiv beschreibt, von besonderem Interesse.
Die stochastischen Algorithmen basieren auf neuen Eulerschen und Lagrangeschen Modellen, die die Bewegung der Partikel in turbulenten Medien beschreiben und auf probabilistischen Darstellungen der Lösungen der Smoluchowski-Koagulations-Gleichung [8].
Die einfachste inhomogene Form der Smoluchowski-Gleichung ist [8]:
und V(t,x) ein stochastisch simulierendes
Vektorfeld der Geschwindigkeit mit gegebener Verteilung ist.
Falls die Koagulation in einer turbulenten Strömung betrachtet wird, ist
die Abschätzung der Partikel-Entwicklung
ein sehr schwieriges und auch noch nicht gelöstes
Problem. Mathematisch kann man dieses Problem als Smoluchowski-Gleichung
mit zufälligen Koeffizienten betrachten [7].
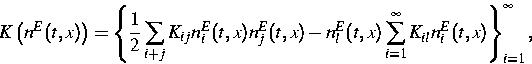
Die stochastischen Lagrangeschen Modelle sind hoch entwickelt im Fall von Ein-Partikel-Verteilungen [14], aber die Entwicklung der Lagrangeschen Zwei-Partikel-Modelle begegnet einer Serie von Schwierigkeiten. Nach Thomson [10] erwähnen wir zwei solche Probleme: (1) das Problem vom eindeutigen Modell, und (2) das ,,Two-to-one Reduction``-Prinzip. Tatsächlich führt die allgemeine ,,Well-mixed Condition`` von Thomson zu einer Serie von verschiedenen stochastischen Differentialgleichungen für die Geschwindigkeit. Es existierten keine mathematischen und auch keine physikalischen Hypothesen, die die Eindeutigkeit garantieren. Und außerdem waren für die existierenden Modelle wichtige physikalische Bedingungen nicht erfüllt. Und daraus folgt, daß Thomsons ,,Two-to-one Reduction``-Prinzip nicht zutreffend war. Diese beiden Probleme wurden in [2], [5], [12] und [14] gelöst: Das Einzigartigkeits-Problem wurde durch eine physikalische Hypothese über die stochastische Struktur der isotropischen Turbulenz behandelt, und es ergab die eindeutige Definition für das System der stochastischen Differentialgleichungen. Um Thomsons ,,Two-to-one Reduction``-Prinzip zu erfüllen, wurde in [2] ein kombiniertes Euler-Lagrangesches stochastisches Modell konstruiert. In [11] wurde die homogene Nukleation in einer fluktuierenden Übersättigung eines Dampf-Felds betrachtet. Die numerische Analysis zeigte, daß die ,,Intermittency`` die Partikel-Zuwachsrate stark beeinflußt.
Die probabilistische Darstellung der Lösung der Smoluchowski-Gleichung wurde in [4] konstruiert und dann in [9] verallgemeinert und geprüft. Die ,,Double Randomization``-Methode für die Smoluchowski-Gleichung mit zufälligen Koeffizienten ist in [6] und [7] dargelegt. Insbesondere sind diese Methoden für eine numerische Analysis der Wirkung der intermittierenden Turbulenz auf die Partikel-Formung geeignet [13].
Damit im Zusammenhang steht die Entwicklung von Methoden dieser Art für die numerische Simulation der chemischen Prozesse gekoppelt mit Koagulation, wie es im Fall der thermischen Zerlegung von Silanen und bei der Tungsten-Hexacarbonyl-Photolysis ist. Eine Theorie der Silane-Zerlegung wurde in [16] und der Tungsten-Hexacarbonyl-Photolysis in [15] entwickelt.
 |
 |
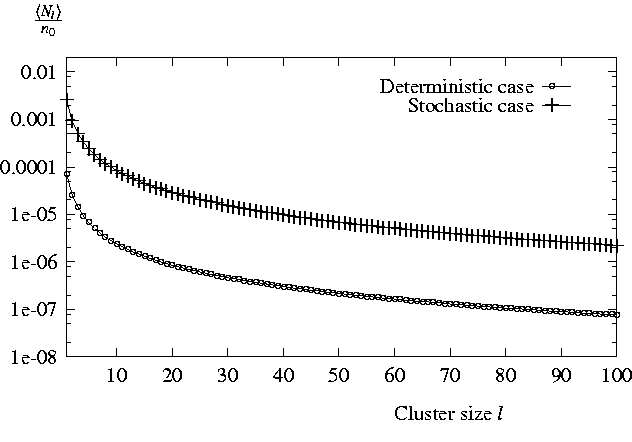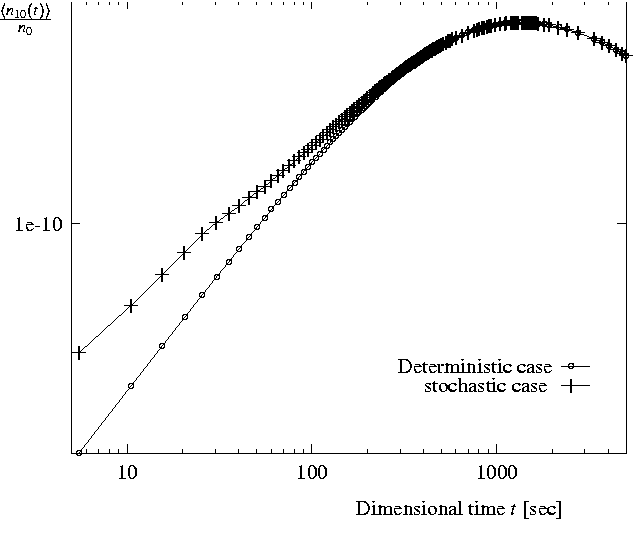
Die Rolle von ,,Intermittency`` ist in Abb. 1 und 2 dargestellt: Das erste Bild zeigt den Fall, wo die Konzentration von 10-mers mit (,,stochastic case``) und ohne (,,deterministic case``) ,,Intermittency`` gerechnet ist. In Abb. 2 ist die Rolle von ,,Intermittency`` sehr groß für Partikel aller Größen.
Projektliteratur:
,One-particle stochastic Lagrangian model for
turbulent dispersion in horizontally homogeneous turbulence,
Monte Carlo Meth. Appl., 4 (1998), No. 2,
pp. 127-140.
|
|
|
[Contents] | [Index] |