



Next: Dimension hyperbolischer Maße
Up:
Previous: Einzugsbereiche hyperbolischer Attraktoren
Bearbeiter: A. Juhl
Kooperation: S. Patterson, U. Bunke, M. Olbrich (Georg-August-Universität
Göttingen),
D. Mayer
(Technische Universität Clausthal), P. Perry (University of Kentucky
at Lexington), A. Deitmar (Ruprecht-Karls-Universität Heidelberg)
Beschreibung der Forschungsarbeit:
Das Ziel dieses Projektes ist die Untersuchung der Dynamik des
geodätischen Flusses Riemannscher Mannigfaltigkeiten negativer
Krümmung. Der geodätische Fluß dieser Mannigfaltigkeiten ist ein
Modell der hyperbolischen Hamiltonschen Dynamik. Die hier betrachteten
Systeme sind stark chaotisch. Die diesen Dynamiken zugeordneten
Zeta-Funktionen sind eng mit den verschiedenen Aspekten der chaotischen
Dynamik verbunden.
Im Fall des geodätischen Flusses von lokal-symmetrischen Räumen sind die
Zeta-Funktionen meromorphe Funktionen einer komplexen Variablen, und das
Hauptproblem der Theorie besteht in der Beschreibung ihrer Nullstellen und
Polstellen.
Für die Untersuchung der Zeta-Funktionen stehen die Methoden der
harmonischen Analysis und der hyperbolischen Dynamik zur Verfügung, und
seit Ruelle's Arbeit [5] ist es eines der herausfordernden Probleme
dieses Gebietes, die Verbindungen der beiden Methoden zu verstehen. Der
Unterschied zwischen den beiden Methoden sei durch die Tatsache
veranschaulicht, daß im Fall des geodätischen Flusses von
hyperbolischen Mannigfaltigkeiten unendlichen Volumens der Einsatz der
harmonischen Analysis extrem kompliziert ist, wohingegen die Ruellesche
Methode der Transfer-Operatoren vom kompakten Fall fast direkt auf den
allgemeineren Fall unendlichen Volumens ausgedehnt werden kann.
Es war das Anliegen dieses Langzeitprojektes, die Verbindungen zwischen den
verschiedenen Zugängen zu verstehen und auf dieser Grundlage den
geodätischen Fluß hyperbolischer Mannigfaltigkeiten unendlichen Volumens
zu untersuchen.
Der grundlegende methodische Ansatz ist hierbei der einer Kohomologie-Theorie
der Zeta-Funktionen, wie sie von vorangegangenen Ergebnissen zu einer
kohomologischen Theorie der Zeta-Funktionen
([3],[7]) nahegelegt wurden.
Hierzu war es jedoch notwendig, die in [3] eingesetzten
Methoden,
die auf der
Theorie der unendlich-dimensionalen Darstellungen Liescher Gruppen basieren,
durch einen alternativen Zugang von differential-geometrischer/dynamischer
Natur zu ersetzen. Somit war das Hauptproblem die Suche nach einer
Beschreibung der Nullstellen und Polstellen der Zeta-Funktionen durch
Invarianten, die der Dynamik auf dem unterliegenden Phasenraum
kanonisch zugeordnet sind.
In den Jahren 1994/1995 fand der Bearbeiter eine derartige Charakterisierung
im Fall der Zeta-Funktionen kompakter hyperbolischer Räume mit Hilfe von
Differentialformen mit distributiven Koeffizienten (Ströme), die ein
System von partiellen Differentialgleichungen erfüllen, welches kanonisch
durch die unterliegende hyperbolische Hamilton-Struktur bestimmt ist.
Diese Gleichungen ersetzen die Bohr-Sommerfeldschen Quantisierungs-Bedingungen
im vollständig integrierbaren Fall. Weiterhin stellte es sich heraus,
daß die neue Theorie der Ströme ein natürlicher Teil einer Hodge-Theorie
der stabilen Blätterung des Phasenraumes ist. Obwohl diese Hodge-Theorie
in vieler Hinsicht der Hodge-Theorie elliptischer Komplexe ähnelt, zeigen
sich hier viele neue Erscheinungen. Insbesondere ist die technische
Seite der Theorie völlig andersartig als im elliptischen Fall.
Diese Ergebnisse führten auf die Formulierung eines Systems von Vermutungen
zur Beschreibung der Singularitäten der Zeta-Funktionen von hyperbolischen
Mannigfaltigkeiten unendlichen Volumens. Der neue Aspekt im Fall unendlichen
Volumens ist der, daß die für die Singularitäten verantwortlichen Ströme
ihren Träger nur im stabilen Basin des Flusses haben.
Zu Beginn des Jahres 1996 fanden U. Bunke und M. Olbrich eine Beschreibung der
Singularitäten der Zeta-Funktionen durch die Gruppen-Kohomologie von
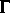 auf endlichen Keimen holomorpher Familien von Hyperfunktionen
auf der Limesmenge einer Kleinschen Gruppe
auf endlichen Keimen holomorpher Familien von Hyperfunktionen
auf der Limesmenge einer Kleinschen Gruppe 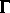 . Diese Beschreibung
entspricht einer Vermutung von Patterson ([8],[2]). Der
Beweis erforderte die
Entwicklung neuer Techniken. Hierbei waren die Ergebnisse in
[5] wichtig.
. Diese Beschreibung
entspricht einer Vermutung von Patterson ([8],[2]). Der
Beweis erforderte die
Entwicklung neuer Techniken. Hierbei waren die Ergebnisse in
[5] wichtig.
Diese Ergebnisse waren nun eine ideale Grundlage für einen Test der von uns
entwickelten Vermutungen, und mit Hilfe einer neuen Methode zur Konstruktion
invarianter Distributionen auf den Limesmengen war es möglich, die
Verträglichkeit aller bisher vorliegenden Ergebnisse mit den Vermutungen
zu beweisen. Damit sind nun wichtige Teile der Vermutungen bewiesen.
Insbesondere ist jetzt klar, wie die Resonanzen des Laplace-Operators der
hyperbolischen Mannigfaltigkeit mit Distributionen auf der
Limesmenge verbunden sind und was diese mit den Strömen auf dem stabilen
Basin zu tun haben. Analog dazu steht auch der topologische Teil der
Singularitäten der Zeta-Funktionen mit Differentialformen auf der
Limesmenge in Verbindung.
Das gesamte Material dieser Theorien und ihrer Verbindungen zu den klassischen
Theorien ist in der Monographie [4] dargestellt.
Bei allem Fortschritt ist jedoch gegenwärtig z. B. die vollständige
Untersuchung der Zeta-Funktion
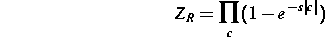
des geodätischen Flusses einer Kleinschen Mannigfaltigkeit noch nicht
möglich, da viele technische Probleme noch ungelöst sind. Die in
[4] formulierten Prinzipien geben jedoch die Leitlinien
für die weitere Untersuchung dieser (und anderer) Funktionen.
Projektliteratur:
- U. Bunke, M. Olbrich, Selberg Zeta and
Theta functions. A differential
operator approach, Mathematical Research, vol. 83,
Akademie-Verlag, 1995.
- U. Bunke, M. Olbrich,
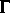 -cohomology
and the Selberg zeta function, J. Reine Angew. Math., 467
(1995), pp. 199--219.
-cohomology
and the Selberg zeta function, J. Reine Angew. Math., 467
(1995), pp. 199--219.
- A. Juhl, Index-Theorie und hyperbolische
Dynamik, Habilitationsschrift, Humboldt-Universität zu Berlin, 1993.
- A. Juhl, An introduction to the cohomological theory of dynamical zeta
functions, in Vorbereitung.
- S. Patterson, On Ruelle's zeta function,
Festschrift in honor of I. I. Piatetski-Shapiro
on the occasion of his sixtieth birthday (S. Gelbart, R. Howe, and
P. Sarnak, eds.), Weizmann Science Press, Jerusalem, 1990, pp. 163--184.
- S. Patterson, Two conjectures on Kleinian
groups, Vortragsmanuskript, Warwick, März 1993.
- P. Perry, S. Patterson, The divisor of
zeta functions for Kleinian groups, erscheint in: Invent. Math.
- D. Ruelle, Zeta functions for expanding maps
and Anosov flows,
Invent. Math., 34 (1976), pp. 231--242.




Next: Dimension hyperbolischer Maße
Up:
Previous: Einzugsbereiche hyperbolischer Attraktoren
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
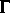 auf endlichen Keimen holomorpher Familien von Hyperfunktionen
auf der Limesmenge einer Kleinschen Gruppe
auf endlichen Keimen holomorpher Familien von Hyperfunktionen
auf der Limesmenge einer Kleinschen Gruppe 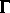 . Diese Beschreibung
entspricht einer Vermutung von Patterson ([8],[2]). Der
Beweis erforderte die
Entwicklung neuer Techniken. Hierbei waren die Ergebnisse in
[5] wichtig.
. Diese Beschreibung
entspricht einer Vermutung von Patterson ([8],[2]). Der
Beweis erforderte die
Entwicklung neuer Techniken. Hierbei waren die Ergebnisse in
[5] wichtig.




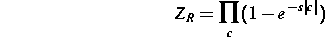
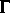 -cohomology
and the Selberg zeta function, J. Reine Angew. Math., 467
(1995), pp. 199--219.
-cohomology
and the Selberg zeta function, J. Reine Angew. Math., 467
(1995), pp. 199--219.